GRAFICACIÓN
3D
REPRESENTACION
DE OBJETOS EN TRES DIMENSIONES
La representación gráfica en 3D ofrece la
posibilidad de crear mundos virtuales en un ordenador, lo cual unido a la
visualización permite al usuario explorar y entender, rápidamente, sistemas complicados.
Esto es posible gracias al avance de lenguajes orientados a objetos, que
ofrecen la posibilidad de crear software de mejor calidad y más fácil de
mantener.
Entre las diferentes herramientas de visualización,
representación 3D y procesamiento de imágenes, cabe destacar VTK (Visualization
Toolkit), código abierto cuyo núcleo está implementado en C++ y que soporta envolturas
(“wrappers”) para TCL, Python y Java; permitiendo el desarrollo de aplicaciones
complejas de un modo eficiente y mediante scripts sencillos. Por todo ello, VTK
se emplea en la visualización médica, la visualización industrial,
reconstrucción de superficies a partir de digitalización láser o nubes de puntos
desorganizados, etc.
En lo que sigue veremos los conceptos básicos
en los que se basa VTK para poder generar una escena y, mediante una serie de
ejemplos, desarrollados en Python, llegaremos a crear nuestras propias escenas
de visualización.
VISUALIZACION
DE OBJETOS
Existen distintos modos de entender lo que es
una "grafica tridimensional", aunque todos se refieren a
ilustraciones que -en realidad- son solo bidimensionales. La forma ms conocida
-y antigua- es la estereoscópica, que se basa en la diferente visión de los dos
ojos y produce el efecto de profundidad mediante lentes con filtros rojo y
verde (uno para cada ojo).
Otra estuvo en pleno auge hace un par de años y
se conoce como "auto estereograma": son los "puntitos" que
no parecen representar nada pero, con buenos ojos, paciencia, esfuerzo para
desenfocar la vista (...y posteriores posibles dolores de cabeza) permiten ver
figuras con "profundidad".
Ambas técnicas se benefician hoy del computador
para su producción. Pero ninguna de estas permite obtener varias vistas de un
mismo objeto o de un mismo paisaje.
La técnica para esto es otra: es la que usan
arquitectos e ingenieros para diseñar edificios, muebles y máquinas. En otras
palabras, se necesitan planos o, ms precisamente, juegos de coordenadas de
todos los vértices, ecuaciones que representen los vectores (aristas rectas o
curvas) y muchos, muchos cálculos para hacer aparecer un objeto en cierta posición
y luego en otra. Y aún más instrucciones y cálculos para posicionar fuentes de
luz, proyectar sombras, ajustar colores en función de la distancia, etc. Esto
es lo que hizo las aplicaciones profesionales de CAD (diseño asistido por
computador) primero en grandes computadores o en máquinas especializadas
(estaciones gráficas) y hoy se están popularizando como aplicaciones de 3D al
alcance de cualquier aficionado. Por cierto se necesita siempre cierto
"poder de cómputo" y no cualquier Macintosh o PC sirve.
TRANSFORMACIONES
TRIDIMENSIONALES
Las transformaciones tridimensionales se pueden
representar con matrices de 4 X 4, siempre y cuando usemos representaciones de
coordenadas homogéneas de los puntos en el espacio tridimensional. Así, en
lugar de representar un punto como (x, y, z), lo hacemos como (x, y, z, W),
donde dos de estos cuádruplos representan el mismo punto si uno es un
multiplicador distinto de cero del otro: no se permite el cuádruplo (0, 0, 0,
0). Como sucede en el espacio bidimensional, la representación estándar de un
punto (x, y, z, W) con W ≠ 0 se indica (x/W, y/W, z/W, 1).
La transformación de un punto a esta forma se denomina
homogeneización, igual que antes. Además los puntos cuya coordenada W es cero
se llaman puntos en el infinito.
Las transformaciones geométricas
tridimensionales que se estudian son tres en concreto: traslación, escalado y
rotación.
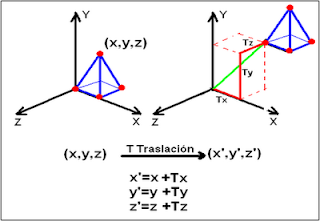
TRASLACIÓN
Nos permitirá cambiar la posición de un objeto,
moviéndolo en línea recta desde una posición inicial a la posición final.
Requiere 3 parámetros:
Tx = Desplazamiento en X
Ty = Desplazamiento en Y
Tz = Desplazamiento en Z
Las nuevas coordenadas se obtienen mediante las
siguientes ecuaciones:
x’= x+Tx
y’= y+Ty
z’= z+Tz
Donde:
Tx, Ty,Tz > 0 Desplazamiento positivo
Tx, Ty,Tz < 0 Desplazamiento negativo
Tx,Ty,Tz = 0 No hay desplazamiento
La matriz que utilizamos en la Traslación es
de la forma:
Y al realizar la matriz el resultado grafico es
el siguiente:
ESCALACION
La matriz para la transformación de escalación
de una posición P = (x, y, z) con respecto del origen de las coordenadas.
Consiste en cambiar el tamaño de un objeto. Las nuevas coordenadas se obtienen
mediante las siguientes ecuaciones:
− x’= x Sx
− y’= y Sy
− z’= z Sz
Requiere 3 parámetros:
Sx = Factor de escalación en X
Sy = Factor de escalación en Y
Sz = Factor de escalación en Z
Sx,Sy,Sz > 1 Aumenta la dimensión
Sx,Sy,Sz < 1 Disminuye la dimensión
Sx,Sy,Sz = 1 Se mantiene la dimensión
La matriz que se utiliza para la escalación es
de la forma:
La resultante de la matriz dentro de una
grafica tridimensional seria:
ROTACIÓN
Para generar una transformación de rotación,
debemos designar un eje de rotación respecto del cual girara el objeto, y la
cantidad de rotación angular, es decir, un ángulo (θ).
Una rotación tridimensional se puede
especificar alrededor de cualquier línea en el espacio.
Los ejes de rotación más fáciles de manejar son
aquellos paralelos a los ejes de coordenadas.
Los ángulos de rotación positiva producen giros
en el sentido opuesto a las manecillas del reloj con respecto al eje de una
coordenada, si el observador se encuentra viendo a lo largo de la mitad
positiva del eje hacia el origen de coordenadas.
Los ángulos de rotación positiva producen giros
en el sentido opuesto a las manecillas del reloj con respecto al eje de una
coordenada, si el observador se encuentra viendo a lo largo de la mitad
positiva del eje hacia el origen en coordenadas.
Se forma una matriz de rotación inversa al
sustituir el ángulo de rotación θ por –θ. Los valores negativos para los
ángulos de rotación generan rotaciones en una dirección en el sentido del
reloj, de modo que se produce la matriz identidad cuando se multiplica
cualquier matriz de rotación por su inverso.
Consiste en girar un objeto alrededor de uno de
los ejes de coordenadas. Respecto al eje Z
Por ejemplo, las nuevas coordenadas se obtienen
mediante las siguientes ecuaciones:
− x’= x cos(α)- y sen(α)
− y’= x sen(α)+ y cos(α)
− z’= z
Donde α es el ángulo de giro
Las matrices que se utilizan para cada eje de
coordenadas son las siguientes:
Y gráficamente los resultados son:
Rotación con respecto al eje X
Rotación con respecto al eje Y
Rotación con respecto al eje Z
COMPOSICION DE TRANSFORMACIONES TRIDIMENCIONEALES
La composición de transformaciones
tridimensionales es la transformación de dos traslaciones sucesivas.
Es decir que resulta de la multiplicación de
nuestra matriz de puntos de la figura original, por el resultado de la
multiplicación de la matriz de la primera traslación por la matriz de la
segunda traslación.
De esta manera de estas operaciones matriciales
obtenemos los nuevos puntos de nuestra figura trasladada.
LINEAS Y
SUPERFICIES CURVAS
Las representaciones de líneas y superficies
son de aplicación a los procesos de diseño de formas y de desarrollo de planos
constructivos. A los tradicionales puntos de vista de si debe determinarse la
enseñanza para todas las aplicaciones o por el contrario si debe consistir en
una formación de gran contenido geométrico-proyectivo se une la utilización de
ordenadores. Para conjugar estas tendencias el autor expone la representación
de curvas y superficies de aplicación técnica: Punto, recta, plano,
circunferencia, otras curvas planas, hélice cilíndrica, poliedros regulares,
superficies radiadas, esfera, etc. El estudio de algunas superficies como las
desarrollables, muy importantes en los trazados de construcción naval.
Finalmente analiza las ecuaciones analíticas, absolutamente imprescindibles
para su representación por ordenador.
Los métodos más eficientes para determinar la
visibilidad de objetos con superficies curvas son la proyección de rayos y los
métodos basados en árbol octal. Con la proyección de rayos, calculamos las
intersecciones entre los rayos y las superficies y localizamos la distancia de
intersección más pequeña a lo largo del trayecto del rayo. Con los arboles
octales, simplemente exploramos los nodos de adelante hacia atrás para
localizar los valores de color de superficie. Una vez definida una
representación en árbol octal a partir de las definiciones de entrada de los
objetos, todas las superficies visibles se identifican con el mismo tipo de
procesamiento.
No es necesario realizar ningún tipo especial
de consideración para diferentes tipos de superficies, ya sean curvas o de
cualquier otra clase. Una superficie curva también puede aproximarse mediante
una malla poligonal, y entonces podemos utilizar algunos de los métodos de
identificación de superficies visibles previamente expuestos. Pero para algunos
objetos, como las esferas, puede que sea más eficiente, además de más preciso
utilizar el método de proyección de rayos y las ecuaciones que describen la
superficie curva.
Representación de superficies curvas Podemos
representar una superficie como una ecuación implícita de la forma
f(x,y,z)=0
O con una representación peramétrica. Las
superficies de tipo spline, por ejemplo, se suelen describir mediante ecuaciones para métricas.
En algunos casos, resulta útil obtener una
ecuación explicita de la superficie, como por ejemplo una ecuación que nos de
la altura con respecto a un plano de tierra xy: Z=f(x,y) Muchos objetos de
interés, como las esferas, elipsoides, cilindros y conos tienen representación
mediante ecuaciones cuadráticas.
Estas superficies se suelen utilizar comúnmente
para modelar estructuras moleculares, cojinetes, anillos y ejes. Los algoritmos
de líneas de barrido y de proyección de rayos requieren a menudo técnicas de
aproximación numérica para resolver la ecuación de la superficie en el punto de
intersección con una línea de barrido o con un rayo de un pixel. Se han
desarrollado diversas técnicas, incluyendo cálculos en paralelo e
implementaciones hardware de gran velocidad, para resolver las ecuaciones de
intersección con superficies curvas para los objetos más comúnmente utilizados.
Superficies cuadráticas
Una clase de objetos que se utiliza con
frecuencia son las superficies cuadráticas, se describen con ecuaciones de
segundo grado (cuadráticas). Incluyen elipsoides, toros, paraboloides e hiperboloides.
Las superficies cuadráticas particular las esferas y elipsoides, son elementos
comunes de las escenas gráficas y es frecuente que estén disponibles en los
paquetes de gráficas como primitivc los cuales se pueden elaborar objetos más
complejos.
Esfera
En las coordenadas cartesianas, una superficie
esférica con radio r que se centra en el origen de las coordenadas se define
como el conjunto de puntos (x, y, z) satisfacen la ecuación eje de x2 + y2 + z2
= r2. También podemos describir la superficie esférica en forma paramétrica, al
utilizar los ángulos de latitud y longitud (figura 10-8): x = r cos, -7r/2 <
$< ir/2
y = r eos $sen0, -77 < 8 < TT 2 = rsen
La representación paramétrica en las ecuaciones
10-8 proporciona un rango simétrico para los parámetros angulares 6 y. En forma
alternativa, podríamos despejar las ecuaciones paramétricas al utilizar coordenadas
esféricas estándar, donde el ángulo 6 se especifica como la latitud. Entonces,
0 se define obre el rango O < ó < K, y 0 con frecuencia se toma en el
rango O < 0 < 2n. También > podríamos establecer la representación al
utilizar los parámetros u y v definidos obre el rango de O a 1 al sustituir § -
nú y 0 = 2iw.
Elipsoide
Una superficie elipsoide se puede describir
como una extensión de una superficie esférica, donde los radios en tres
direcciones mutuamente perpendiculares entre si. una representación paramétrica
para la elipsoide en términos del ángulo de ititud $ y el ángulo de longitud 6
en la figura 10-8 es x = rv eos eos 9, y = ry coscasen8,
Toro
Un toro es un objeto en forma de dona, como se
ilustra en la figura 10-11. Se puede generar al girar una circunferencia u otro
cónico alrededor de un eje específico. Las presentaciones para métricas para un
toro son similares a las de una elipse, excepto que el ángulo se extiende a lo
largo de 360°. Al utilizar ángulos de latitud longitud <|) y 0, podemos
describir la superficie del toro como el conjunto de puntos eje satisfacen
x = rx(r + eos )cos 8, ~ TT < ^ < TT y =
r (j + cos(/> )sén#, —ir < 0< TT 2 = r,sen
Las llamadas curvas y superficies de Bézier.
Este tipo de curvas y su generalización a superficies proporcionan hoy en día
una de las principales herramientas para la representación de figuras en la
mayoría de aplicaciones del Diseño Asistido por Computador (CAD) y han dado
lugar a una rama de esta disciplina conocida con el nombre de Diseño Geométrico
Asistido por Computador (CAGD).
Las Curvas de Bézier se denominan curva de
Bezier a un método de definición de una curva en serie de potencias. El método
consiste en definir algunos puntos de control, a partir de los cuales se
calculan los puntos de la curva. Describiremos el método de construcción
recursivo conocido como algoritmo de De Castel jau.
Para dos puntos, la curva es un segmento recto,
definido en forma par amétrica por interpolación de los puntos extremos: P =
(1-u)P0 + uP1. Donde los Pi son los puntos de control y uÎ[0,1] el parámetro.
Las curvas de Bezier son adecuadas para representar tramos aislados de una
curva libre cualquiera. Para representar la curva entera, se puede hacer una
unión “suave” de varias curvas de Bezier.
La unión suave de curvas independientes se
denomina spline. Superficies Existen muchas variantes útiles para construir
superficies, la más sencilla de comprender es el producto cartesiano o tensorial
de curvas de Bezier o de NURBS. Para definir una superficie como un producto
cartesiano, debemos asumirla como una función de dos parámetros (u,v): En las
superficies, las condiciones de borde son mucho más importantes que para las
líneas, porque al renderizar se verán efectos luminosos indeseables si la
normal no pasa suavemente de un tramo a otro. Hay muchos tipos de superficies,
pero casi todos pueden traducirse o representarse como NURBS, a veces
recortadas. De hecho la mayoría de los paquetes de software (al menos los mas
técnicos) transforman cualquier otra posibilidad en una NURBS para el
intercambio de archivos
CONCLUSION:
Hoy
por hoy, la representación gráfica 3D y su visualización forman parte de
nuestra vida cotidiana; basta fijarse en el mundo del entretenimiento, en la
industria del juego y en el soporte de hardware y software para tales fines.
¿Quién en su ordenador personal no ha instalado un juego, visto una película,
renderizada en 3D?







No hay comentarios.:
Publicar un comentario